Continued Fractions and Matrices Continued

Today's blog continues a previous blog on how 2x2 matrices can be used to represent continued fractions. The lemmas presented in today's blog are used in the solution to Pell's Equation. For those interested in the background to Pell's Equation, start here. For those who would like to proceed to its solution using continued fractions and matrices, go here. The solution to Pell's Equation is used as part of the proof for Fermat's Last Theorem, n=5.

The content in today's blog is based on Harold M. Stark's An Introduction to Number Theory.

For Lemma 1, α_n, q_n are defined here. For Lemma 2, M_n is defined here.

Lemma 1: α_nq_n-1 + q_n-2 ≠ 0

(1) Assume that α_nq_n-1 + q_n-2 = 0.

(2) Then, q_n-1 = 0 and q_n-2 = 0. [See here for proof]

(3) But q_n ≥ 1 for n ≥ 1. [See here]

(4) Futher, there are no successive 0's in a row since (see here for details on how these values are derived):
q_-2 = 1
q_-1=0
q₀=1

(5) Therefore #2 is impossible and we reject our assumption.

QED

Lemma 2: if γ_n = α_nq_n-1 + q_n-2, then γ_n(1,α) = (1,α_n)M_n

(1) From the definition of M_n (see here), we know that:


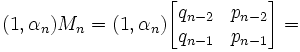
= (q_n-2+α_nq_n-1, p_n-2+α_np_n-1) [See here for review on matrix products]

(2) By applying the equation α = (p_n-2 + α_np_n-1)/(q_n-2 + α_nq_n-1) [See here], we get:

(q_n-2+α_nq_n-1 , p_n-2+α_np_n-1) = (q_n-2 + α_nq_n-1)(1,α)

(3) Adding back γ_n, this gives us:
(q_n-2 + α_nq_n-1)(1,α) = γ_n(1,α)

QED

Lemma 3: if δ = γ_n+j/γ_n, then δ(1,√d) = (1,√d)M_n^-1M_n+kj

(1) From Lemma 2, we know that;

γ_n(1 , α) = (1, α_n)M_n

and

γ_n+j(1, α) = (1, α_n+j)M_n+j

(2) By the definition of matrix inverses (see here), we know that:
(1,α_n)M_nM_n^-1 = (1,α_n)

(3) From #1, then we have:
[(1,α_n)M_n)] = γ_n(1,α)

(4) So, from #2, we have:
(1,α_n) = γ_n(1,α)M_n^-1

(5) Likewise since α_n = α_n+j (see here), we get:
(1,α_n+j)M_n+j = (1,α_n)M_n+j

(6) Applying #4, this gives us:
(1,α_n+j)M_n+j = γ_n(1,α)M_n^-1M_n+j

(7) Combining #1 with #6, gives us:
γ_n+j(1,α) = γ_n(1,α)M_n^-1M_n+j

(8) Now, δ = γ_n+j/γ_n [We can do this since γ_n ≠ 0 (see Lemma 1 above) ]

(9) δ(1,α) = [(γ_n+j)(1 , α)]/γ_n

(10) Applying #7 gives us;

δ(1,α) = [γ_n(1,α)M_n^-1M_n+j]/γ_n =
= (1,α)M_n^-1M_n+j

QED